SBF, Pascal's Mugging, and a Proposed Solution

Thoughts

Nov, 14 2022

Contents

There are some uncommon concepts in this post. See the links at the bottom if you want to familiarize yourself with them. Also, thanks to matt and simon for inspiration and feedback.

Overview

Recently there’s been discussion over how SBF answered Tyler Cowen’s question about the St. Petersburg paradox:

The main idea behind the question is to see how SBF responds to the following apparent paradox:

The game offers a positive expected value return of $2 * .51 + 0 * .49 = 1.02$
It’s clear that if you play this game long enough, you will wind up with nothing. After 10 rounds, there is just a $1/1000$ chance that you haven’t blown up.

How is it that a game with a positive EV return can be so obviously “bad”?

Pascal’s Mugging

A related question is that of pascal’s mugging. You can think of pascal’s mugging as similar to playing Tyler Cowen’s game 100 times in a row. This results in a game of with the following terms:

A $1.046\text{e-}31$ chance of multiplying our current utility by $1.26\text{e}30$.
A $1 - 1.046\text{e-}31$ of everything disappearing.

Should you play this game? Most would respond “no”, but the arithmetic EV is still in your favor. What gives?

Dissolving the Question

The question underlying most discussions of these types of paradoxes is what utility function you should be maximizing.

If your goal is to maximize the increase in expected value, $$ \lim_{t \to \infty} \mathbb{E}\frac{\text{Welfare}_{t}}{\text{Welfare}_0} $$ then you should play the game. There’s no way around the math.

Even though the chance of winning is tiny, the unimaginable riches you would acquire in the event that you got lucky and win push the EV to be positive.

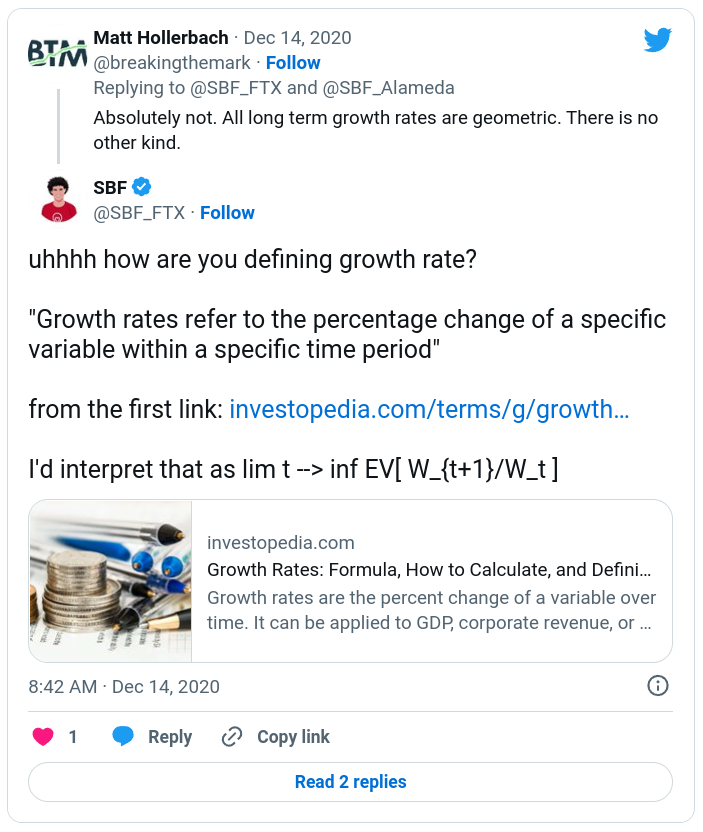
uhhhh how are you defining growth rate?

"Growth rates refer to the percentage change of a specific variable within a specific time period"

from the first link: https://t.co/P6LRrkhBex

I'd interpret that as lim t --> inf EV[ W_{t+1}/W_t ]
— SBF (@SBF_FTX) December 14, 2020

That being said, the formula associated with expected value, the arithmetic mean, is mostly arbitrary. There’s no fundamental reason why the arithmetic mean is what we should aim to maximize. We get to choose what we want to maximize.

An Alternative Function: Log

A common alternative when faced with this issue is to maximize the log of some value. This is a popular choice when maximizing wealth because it incorporates the diminishing marginal utility of money. Some consequences of a log utility function include:

Valuing an increase in wealth from 100,000 to 1M just as much as an increase from 1M to 10M
Valuing a potential increase in wealth of 100 as not worth a potential loss of 100 at even odds.
Valuing a loss leaving you with $0 dollars as completely unacceptable no matter the odds.

While a log function is helpful, incorporates diminishing returns, and can give us a reason to turn down some Pascal’s mugging scenarios, it’s not the perfect solution by itself because it won’t turn down games with exponentially good odds. For example:

Let your wealth by $w$.
Let there be a game with a $p=(1/100)^t$ chance of returning $1000 * e^{w/p} * w$, and a $1-p=1-(1/100)^t$ chance of returning $0.5 * w$.

A log utility function says you should play this game over and over again, but you will most definitely lose all of your money by playing it (with the slim potential for wonderful returns).

What Property Are We Missing?

To find which property we are missing, it’s helpful to build a better intuition for what we are really doing when we maximize these functions.

By maximizing the arithmetic mean, we are:

Maximizing what you would get if you played the game many times (infinitely many) at once with independent outcomes
Maximizing the weighted sum of the resulting probability distribution (this is another way of saying the arithmetic mean)

By maximizing the geometric mean, we are doing the same as the arithmetic mean but on the log of the corresponding distribution.

We are taught to always maximize the arithmetic mean, but when looking at the formulas they represent the question which comes to mind is: Why? Does that really make sense in every situation?

The problem is that these formulas average over tiny probabilities without a sweat, while we as humans only have one life to live. What we are missing is accounting for how:

We don’t care about outcomes with tiny probabilities because of how unlikely we are to actually experience them.
- We ignore bad outcomes which have a less than 0.5% (you can change this number to fit your preferences) left tail lifetime probability of occurring and take our chances. Not doing so could mean freezing up with fear and never leaving the house. One way to think about this is that our lives follow taleb distributions where we ignore a certain amount of risk in order to improve every day life. An example of this is the potential for fatal car accidents. Some of us get lucky, some of us get unlucky, and those who don’t take these risks are crippled in every day life.
- We ignore good outcomes which have a less than 0.5% (you can change this number to fit your preferences) right tail lifetime probability of occurring to focus on things we are likely to experience. Not doing so could mean fanaticism towards some unlikely outcome, ruining our everyday life in the process.
We are risk averse and prefer the security of a guaranteed baseline situation to the potential for a much better or much worse outcome at even odds
- This is similar to the case of ignoring good outcomes which have a less than 0.5% right tail lifetime probability of occurring, but is done in a continuous way rather than a truncation. This can be modeled via a log function.
We become indifferent to changes in utility above or below a certain point
- There’s a point at which all things greater than or equal to some scenario are all the same to us.
- There’s a point at which all things less than or equal to some scenario are all the same to us.

These capture our grudges with pascal’s mugging! With these ideas written down we can try to construct a function which incorporates these preferences.

A Proposed Solution: The Truncated Bounded Risk Aversion Function

In order to align our function with our desires, we can choose to maximize a function where we:

Truncate the tails and focus on the middle 99% of our lifetime distribution (you can adjust the 99% to your preferred comfort level). Then we can ignore maximizing the worst and best things which we are only 1% likely to experience.
Use a log or sub-log function to account for diminishing returns and risk aversion
Set lower and upper bounds on our lifetime utility function to account for indifference in utility beyond a certain point

There we go! This function represents our desires more closely than that of an unbounded linear curve, and is not susceptible to pascal’s mugging.

Notes

This function works pretty well, but there are some notes to be aware of:

This does not mean maximizing the middle 99% of the distribution on each and every decision. Doing so would mean winding up with the same problems as before by repeating a decision with a 0.1% chance of going horribly wrong over and over again, eventually building up into a large percentage. Instead, you maximize the middle 99% over whatever period of time you feel comfortable with. A reasonable choice is the duration of your life.
If you were to have many humans acting in this way, you would need to watch out for resonant externalities. If 10,000 people individually ignore an independent 0.5% chance of a bad thing happening to a single third party, it becomes >99% likely that the bad thing happens to that third party. A way to capture this in the formula is to truncate the middle 99% of the distribution of utility across all people, and factor the decisions of other people into this distribution.
There is a difference between diminishing returns and risk aversion.
- Diminishing returns refers to the idea that linear gains in something become less valuable as you gain more of it. Billionaires don’t value $100 as much as ten year olds for example.
- Risk aversion refers to the idea that we exhibit strong preferences for getting to experience utility. We don’t like the idea of an even odds gamble between halving or doubling our happiness for the rest of our lives. This can be thought of like maximizing the first percentile of a distribution. Log functions cause us to prioritize the well being of lower percentiles over higher percentiles and thus line up with this preference.
A log utility function over the course of your life does not necessarily mean that you approach independent non compounding decisions in a logarithmic way. It’s sometimes the case that maximizing non compounding linear returns will maximize aggregate log returns.

Back To SBF

So back to SBF. How does this affect our response to the St. Petersburg paradox? If your goal is to maximize arithmetic utility in a utilitarian fashion, then the answer is still that you should play the game. On the other hand, if your goal is to maximize utility in a way that factors in indifference to highly unlikely outcomes, risk aversion, and bounded utility, you have a good reason to turn it down.